Fibonacci数列为什么经常出现在植物中
拾起一个松果仔细观察(你问为什么要这么做?如果你不问这个问题而是把这个动作重复上40次,说不定已经发nature了= =注:传说有人去山上捡了40个松果,统计出左旋和右旋型的松果数量是基本相同的,于是发了篇nature[1]),我们至少能在其上找到两种旋转方向相反的螺线。若有人闲得蛋疼,非要数一数这样的螺线有多少条,就图一中的例子来说,是8和13。我们在向日葵的头状花序上也能见到这样的螺线,并且同样可以找出旋转方向相反的两种(通过改变线的连接方式,你也可以找出更多这样的螺线)。数一下条数,小的是13和21,大的是21和34。这些数字看起来似乎不是任意的,彼此之间还有些关联。比如8+13=21,,13+21=34。正如标题所说,这些数字都是Fibonacci数列{1,1,2,3,5,8,13,21,34……}的一部分,并且两种方向相反的螺线数还是Fibonacci数列种相邻的两个数字。把视线稍微放宽一点,植物叶子的排列方式,叫做叶序。最常见的有互生,对生和轮生。如果我们只观察互生(互生的特点是每个节上只有一片叶子),从茎生长的方向垂直看下来,相邻叶片之间往往相差(旋转了)一个角度,从下往上数叶片的数量,直至新数到的叶片角度与初始叶片完全重合。例如在数的过程中叶片转过3圈,共有8片叶子,称为3/8叶序(螺旋叶序)。橡树和梨树的叶序就为3/8,椴树的叶序为1/2,柳树为5/13[4]。从中我们依旧看到Fibonacci数的身影。那为什么植物中存在着这么多的Fibonacci数呢?

图1 松果和向日葵上的螺线
通常的科普会告诉你:“$F_n$表示Fibonacci数列中的第n个数,$\tau=\lim\limits_{n \to\infty} \frac{ F_{n+1}}{F_n} =\frac{ 1+\sqrt{5}}{2}$,也就是传说中的黄金率。$\theta=2\pi/ \tau^2 \approx 137.51^{\circ}$,称为黄金角。两个叶片之间的角度(称为发散角)刚好就是这个黄金角,这使得叶片之间不会相互重叠遮挡,从而能够获取尽可能多的阳光。”这个说法其实有很多问题,首先如果需要叶片非周期不重叠地排列,只要发散角是任意的无理数都可以达到,为什么非得是黄金角不可呢?其次叶片能否接受到尽可能多的阳光,明显和植物所处的生境关系更大。若为了获得最多的阳光,叶片的排列照理来说也需要与叶片的形状相搭配才能达到最大效率。最后多数植物的发散角并不是完美的黄金角。比如3/8叶序。3*360/8=135(转3圈后就会重复,也说明发散角不是无理数)。所以网上常见科普文的解释是完全站不住脚的。
事实上这个问题已经困扰人类上百年,相关的研究成果发在nature或者PRL也都算轻松。数学,物理,生物学对这个问题都有不少研究,观察不同学科对同一个问题的研究方法和侧重点差异本身还是相当有趣的。由于我个人更重视原理层面的解释性,以下给出的解释[3]是数学角度的。选取的标准是这个模型足够说服我,既能解释为什么Fibonacci数经常出现,也能解释存在不属于Fibonacci数但出现频率较少的其他数列,以及如果是一些随意的数组为什么不行,比如向日葵头状花序上的两种螺线条数为什么不能是11,12这样的组合?甚至更近一步为什么有些是3,5,有些是13,21这种组合是否是随意搭配的或者必须满足某些要求?
1准备工作
我们首先需要一点植物学知识作为模型基础。不管是向日葵的花序或者茎上的叶子,都是在植物的小茎尖上形成的,顶端的圆形区域边缘会产生称为原基的细胞,这些原基随后会发育成诸如叶子,花序等各种植物器官。原基生成后会相对于顶点的中心径向移动,见图 2。1992年,Douady and Couder通过磁性油滴实验用纯物理的手段还原出原基出现在圆形区域位置的规则——新原基总是周期性生成的并且出现在圆盘边缘最不拥挤的地方(离其他原基最远处)[2]。我们把这个规则称为最大值原理,这样的描述还太模糊,晚些时候我们会用更数学的语言重新描述。

图2 两张电子显微镜下木兰花顶端图片以及原基示意图
为了简化,我们采用一个半圆柱形$\mathcal{C}=\mathbb{S}^1 \times [0,+\infty )$作为原基与茎关系的表示。原基产生于$\mathbb{S}^1 \times { 0 }$之后向圆柱上方移动。${p_0,p_1,\dots,p_N }$表示原基的集合,其中$p_k=(\theta_k,y_k)$。因为原基是周期性产生的,显然$y_k=ky$, y称为节间距离,是一个固定值。
我们把两个原基产生的时间间隔称为单位时间T。经过一个T时间之后的原基集合用${P_0,P_1,\dots,P_N }$表示。原基在一个T时间的位置变化关系用$\Phi$表示。$P_{k+1}=(\Theta_{k+1},Y_{k+1})=(\theta_k,(k+1)y)$,也就是原来的$p_k$点向上移动了一个y值,同时新下标也+1.$\Theta_0=F(\theta_0,\dots,\theta_N)$,新的原基由之前所有原基位置决定,F是最大值原理相关的。
p是$\mathbb{S}^1 \times { 0 }$上的点,定义$D(p)=min_{1,\dots,N} ||P_k-p||$,也就是说D(p)给出了p点到所有原基中距离最近的那个点的距离值。而我们要找的新原基 则是满足$D(p_0)=max_{p \in \mathbb{S}^1 \times { 0 }} D(p)$的p0点。这样的点有时候不是唯一的。对于给定的点p_k,$||p-p_k||=\sqrt{(\theta_0-\theta_k)^2+(ky)^2}$所以以$\theta_0$为横坐标,p到p_k的距离为纵坐标,可以得到一条开口向上,最低点在$(\theta_k , ky)$(这也是p_k的坐标)的曲线(可以理解成抛物线的纵坐标开方被压缩了)。p点和每一个p_k点都能画出这样一条曲线。最小距离函数D正是所有曲线的下包络(图3中用黑实线表示)。而我们要找的p0点,则一定在黑实线的最高点垂直对下来的地方。而黑实线的最高点,一定是某两条曲线的交点处。设这两条曲线是$p_m,p_n$相关的,这也表示p0到p_m,P_n的距离相等;p0在p_m,P_n连线的垂直平分线上。P_m和P_n一定在P0的左右两边。
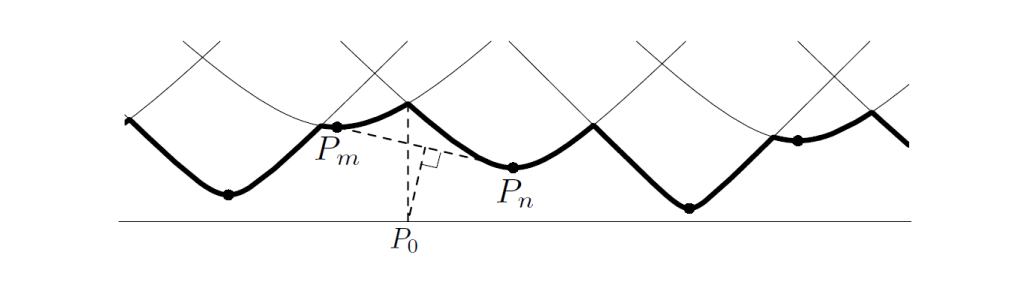
图3
我们所研究的系统具有旋转对称性,坐标起点不是我们需要关心的,我们关心的是点的相对位置。定义发散角$x_k=\theta_{k+1}-\theta_k$.
$$S:(\theta_0, \dots ,\theta_N)\to (\theta_1-\theta_0, \dots ,\theta_N-\theta_{N-1})=(x_0, \dots , x_{N-1})$$
T时间里,用发散角表示的原基变换关系用$\phi$表示,满足关系$S\Phi=\phi S$.
$(X_0, \dots ,X_{N-1})=\phi(x_0, \dots, x_{N-1})$,我们来求$\phi$中的固定点(即使得x=f(x)的x值)。得$x_k=X_k=x_{k-1}$.这表明所有x_k都相等,即发散角为常数值。发散角和节间距离都为定值,形成的点的排列称为螺旋点阵(helical lattices)。进一步可以证明$\phi$中所有固定点都是稳定的。所以我们可以只考虑发散角为定值的情形,这也与植物中观察到的情况一致。
2.1点阵的定义
螺旋点阵L(x,y)是圆柱上由单一固定元素(x,y)生成的离散子群。对应到我们研究的问题,x为发散角,y为节间距离。我们可将圆柱上的点阵在平面上展开,得到一个平面点阵。与L(x,y)相对应的平面点阵称为$\Lambda(x,y)$.它是由(x,y)和(1,0)两个元素生成的。
$$\Lambda(x,y)={ k(x,y)+d(1,0)| k,d \in \mathbb{Z} }$$
我们也将使用复数表示z=x+iy,相对应,$\Lambda(z)$同$\Lambda(x,y)$
如果把$\Lambda(z)$上的点再投影回圆柱上(-1/2<x<=1/2)。我们有$z_k=\delta_k+iky=kx-\Delta_k+iky=kz-\Delta_k$,其中$\Delta_k$为和kx最接近的整数,如果这样的整数有两个选择最小的那个。如下图所示
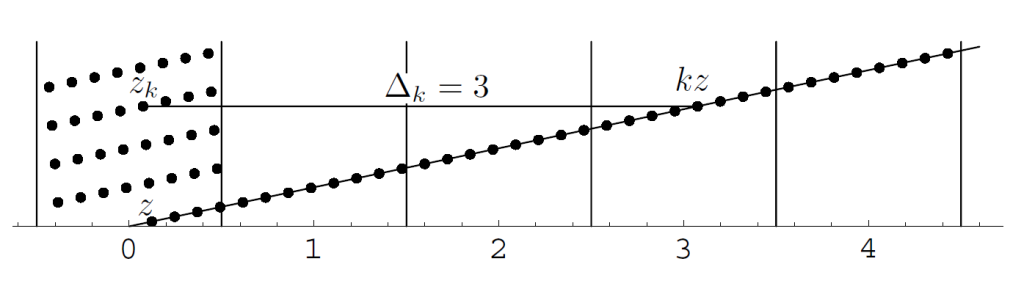
图4
螺旋点阵上的一点$p_k=(\delta_k,ky)$。从原点到p_k的连线可以形成一个缠绕螺旋线,若原点和p_k之间没有其他点存在,这条螺旋线称为k-斜列线。如果有点p_i在原点和p_k之间,i肯定小于k,所以这条螺旋线就应该叫i-斜列线。水平平行移动一个x的长度我们还可以得到另一条k-斜列线。因为p_k的高度为k个单位y,也表示平移k次我们才会碰到最初的那条k-斜列线,所以$L(z)$中我们一共有k条k-斜列线。
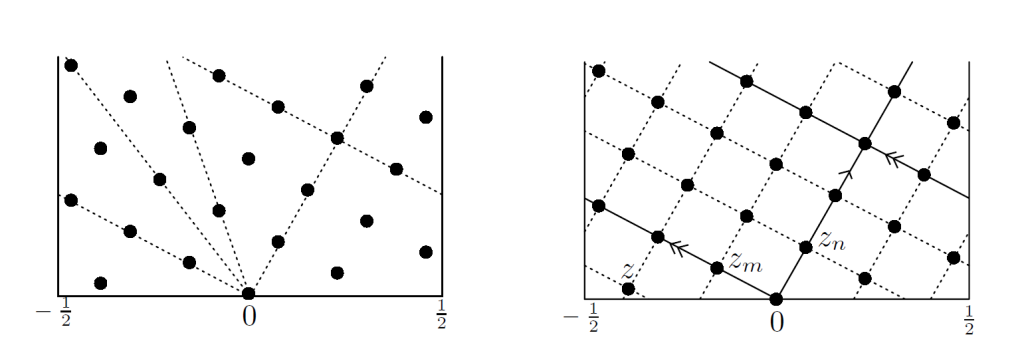
图5
然后我们把讨论范围扩展到平面点阵。从原点出发得到的各种斜列线中,选择其上点阵元素离原点最近的两条。这两个点阵元素需在不同的两条斜列线上,表示为{$z_m,z_n$}.这形成了平面点阵$\Lambda(x,y)$的一组基($z_m=mz-\Delta_m$,它可以是由d不等于0为起点生成的),称为规范基(canonical basis)。这组基所延展出的m,n-斜列线,恰好就是各种植物螺线图案中,人眼最容易识别到的。原因就在于点阵元素的间隔最近,其他点阵元素的距离就想对远一点,具体到一些植物上,因为点阵元素往往不只是一个点,而是有一定形状和面积的单元。离得近通常两个单元就是紧紧挨着的中间不会有其他单元穿插其中,离得远的单元之间,通常有属于其他元素的单元横隔其中。所以人眼不会优先识别这样的螺线。
如果{$z_m,z_n$}满足$max(|z_m|,|z_n|)<2 min(|z_m|,|z_n|) $(注:原论文中此处为$min(|z_m|,|z_n|)<2 max(|z_m|,|z_n|) $,两个正数中小的一个比两个数中大的的两倍小,这完全是句废话,所以这个地方肯定是打错了。),那么{$z_m,z_n$}称为规范斜列线基(canonical parastichy basis)。如果$|z_m|=|z_n|$,那么{$z_m,z_n$}称为菱形规范基。此时的$\Lambda(z)$是一个菱形点阵。
2.2点阵的分类
将圆柱展开后,得到的是一个上半复平面$\mathbb{H}$,这也是一个双曲平面。我们将根据斜列线数对点阵进行分类。 令$z \in \mathbb{H}$使得{z,1}可以作为一组规范基生成一个点阵$\Lambda(z)$。{z,1}及其生成的阵列,可以作为一个生成元或者原型给出我们实际想要研究的任意{$z_m,z_n$}点阵。所以我们有必要先了解其性质。$A=-1/2+i\sqrt{3}/2$,$B=1/2+i\sqrt{3}/2$,把无穷远看作一个点。以0A∞B四个点为顶点,组成了一个双曲四边形,我们记为Q。0A,0B是圆心分别为-1,1,半径为1的圆上的一段圆弧。A ∞,B∞为垂直的射线。AB之间的灰色线是圆心在0点半径为1的一段圆弧。Q中和原点距离大于等于1的点的集合称为$Q^+$,和原点距离小于等于1的点的集合称为$Q^-$。Q中和原点距离在1/2到2之间的区域称为H,是一个双曲六边形。
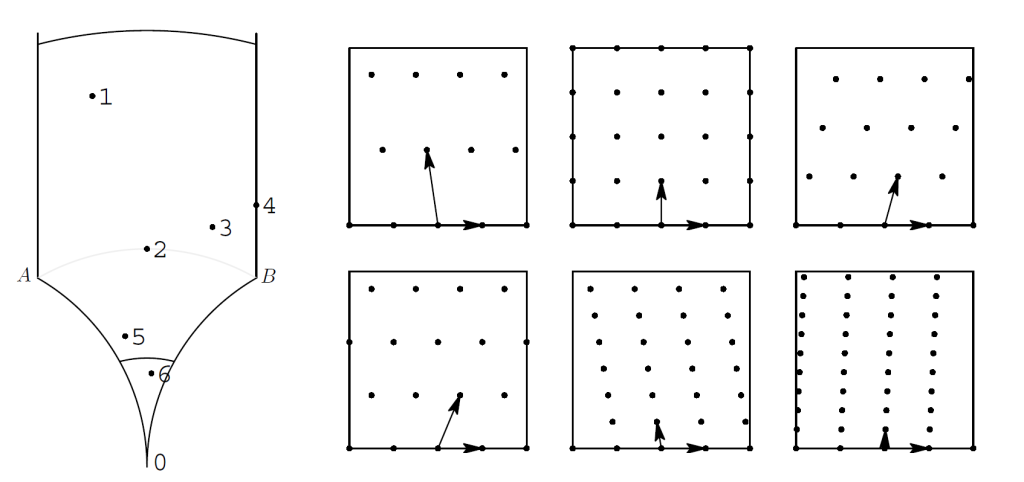
图6
我们有以下命题1成立:
命题1
(i){z,1}是规范基,iff$z \in Q$.
(ii){z,1}是斜列基,iff$z \in H$.
(iii){z,1}是菱形基,iff z在Q中的单位圆弧上(灰线上).
然后我们来看看{$z_m,z_n$}与{z,1}的关系:
定义$g_{mn}(w)=\frac{\Delta_n w-\Delta_m}{nw-m}$,同时Re(z)属于(0,1)
我们有如下的命题2成立
命题2
(i){$z_m,z_n$}是$\Lambda(z)$的一对规范基 iff $z \in Q_{mn}=g_{mn}(Q)$ 同时$\Delta_m, \Delta_n$是使得$\Delta_m n -\Delta_n m=1$成立的唯一整数s,$[\Delta_n/n,\Delta_m/m] \subset [0,1]$
(ii){$z_m,z_n$}是$\Lambda(z)$的一对斜链基 iff$z \in H_{mn}=g_{mn}(H)$
(iii)斜列数为m,n的菱形点阵是Q中的菱形点阵在$g_mn$作用后的像。
我们来看看命题2大概讲了些什么。首先$g_{mn}$是一个变换,把双曲四边形Q变换为另一个双曲四边形$Q_{mn}$,如果需要一个感性认识可查看图9。0变换后变为$\Delta_m/m$,无穷远点变换后变为$\Delta_m/m$,$A \to A_{mn},B \to B_{mn}$,通过计算可知道B_mn会在A_mn的上方。命题2大体是在说{$z_m,z_n$}是$\Lambda(z)$的一对规范基等价于 $z \in Q_{mn}=g_{mn}(Q)$。 存在一个w属于Q,使得$z=g_{mn}(w)=\frac{\Delta_n w-\Delta_m}{nw-m}$,我们可以反向得到$w=\frac{mz-\Delta_m}{nz-\Delta_n}=z_m/z_n$.由命题1$z_m/z_n \in Q$对应就有{w,1}是规范基,即{z_m,z_n}是规范基(这里z_m,z_n顺序或者说方向是有要求的,需要与{z,1}一致,为了简化我给省略了)
像$g_{mn}$这样具有形式$w \to \frac{aw+b}{cw+d}$的映射,称为mobius变换。abcd都为实数,且ad-bc>0时,这个变换是在双曲平面上是保距的。当ad-bc=1,这样的g_mn构成了PSL(2,Z)的一个子群。Q_mn在双曲几何中是全等于Q的,同理H_mn也全等于H,见图7,所有的Q_mn=g_mn(Q)构成了上半复平面H的一个密铺。特别地$g_{11}=1/(1-w)$。将AB代入g_11计算可以得到$A_{11}=1/2+\sqrt{3}/6i,B_{11}=1/2+\sqrt{3}/2i$.两个点的实值部分相同,所以形成的连线会是垂直与x轴的直线。观察图7,通过垂直的灰线,你应该能马上发现Q11。然后所有双曲四边形Q_mn的对角线,即连接AB的灰色圆弧,的并集形成了一个二叉树,称为van Iterson diagram,见图8。ps:值得一提的与Q_11相关的的规范基是两个{z_1,z_1},且两个z_1并不相同,他们一个是z,另一个就是z-1(来自不同d值生成的点)
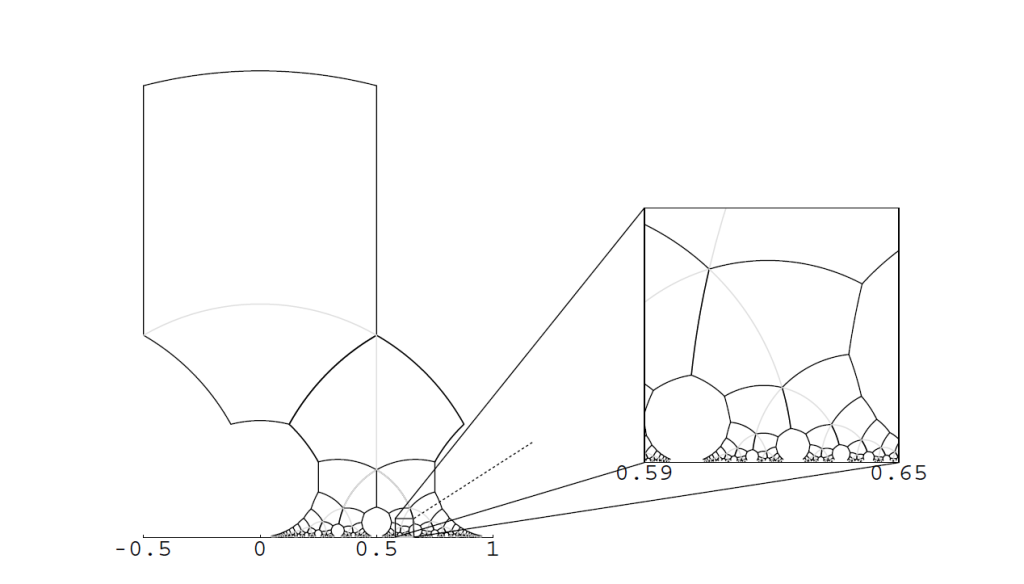
图7
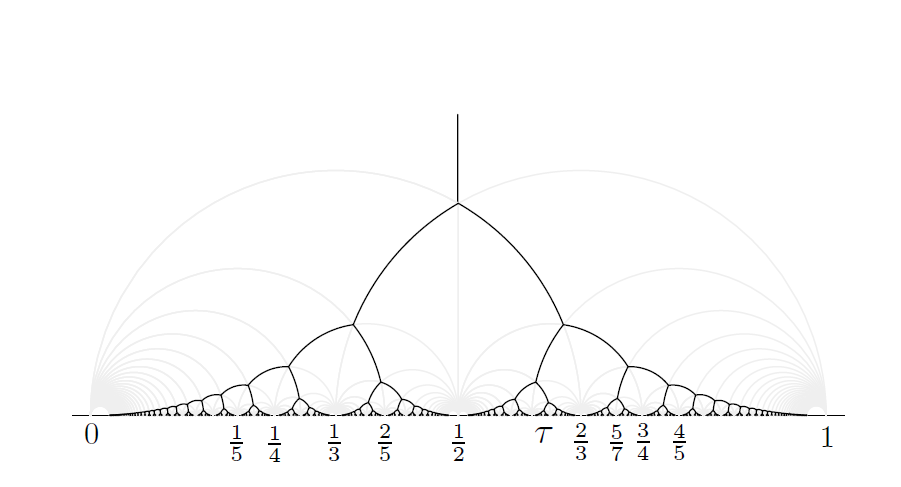
图8
2.3 van Iterson diagram的分岔点
van Iterson diagram是一个二叉树。其上的每一点,都给出了一个菱形点阵。我们可以观察到它在Q中的A点发生分岔。为了帮助我们理解van Iterson diagram,我们需要先了解下变换前A点附近的情况。以下讨论见图9,A点其实是3个双曲四边形的焦点。我们定义两个映射$\alpha:w \to w-1 ,\beta : w \to w/(1-w)$然后$L=\alpha (Q),R=\beta (Q)$,即为我们在图9中观察到的两个双曲四边形。
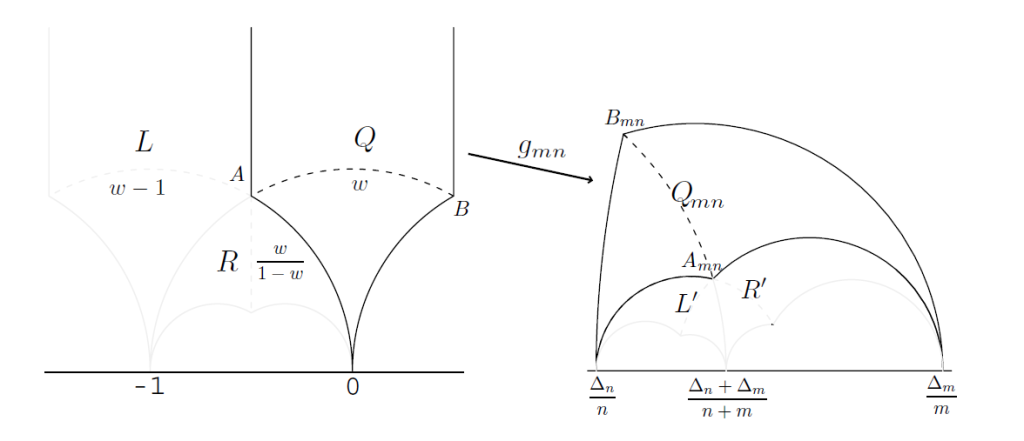
图9
定义$L’=g_{mn}(L), R’=g_{mn}(R)$,我们有如下的引理1,2和命题3成立
引理1:$\Delta_m+\Delta_n=\Delta_{m+n}$
引理2:$g_{m+n,n}=g_{mn}(\alpha ),g_{m,m+n}=g_{mn}(\beta)$
命题3:$R’=Q_{m,m+n} $和$L’=Q_{m+n,n} $
结合图9我们来看看从中得到了哪些信息。首先g变换是不改变拓扑关系的。R和Q原本的共同边A0,变换后依旧邻接,L和Q之间的A∞也是相同。有命题3可知,L,R的g变换都可以由Q的g变换表示,并且给出了变换关系。这也给出了分岔图中在一个分岔点附近,分岔前和分岔后灰线的关系。每一个Q_mn,由于上面提到的邻接关系,下方一定会有另外两个双曲四边形,并且这两个双曲四边形一定是$Q_{m,m+n}$和$Q_{m+n,n}$.值得一提的是$g_{11}=\alpha^{-1} \beta$,不难看出$\alpha ,\beta$生成整个PSL(2,Z).
3分岔图
到此我们终于快接近最初问题的谜底了。不过在此之前我们还需要先介绍一点概念
我们定义Fibonacci-like序列${f_j}$ 为满足$f_j=f_{j-1}+f_{j-2}$的序列.Fibonacci数列我们则用{F_j}表示。{F_j}是初始元素为1,1的Fibonacci-like序列。
如果(2n-m)(2m-n)>0,我们称Q_mn为regular的.反之,我们称它为irregular。 假设m<n,2m<m+n<2n总是成立的。我们可以知道 $Q_{m+n,n}$ 是regular,而 $Q_{m,m+n}$ 是irregular。也就是说对于任意的一个Q_mn(m不等于n),它下方临接的两个曲边四边形,必然一个属于regular,另一个属于irregular。 到这里我们已经有了不少关于格点和分岔图性质的了解了。是时候回到植物与原基的问题上来了。对原基真正特别的地方其实也只有最大值原理。 回忆最大值原理要求我们什么。新生的原基一定在两个其他原基的垂直平分线上。也就是p0到p_m,P_n的距离相等;P_m和P_n一定在P0的左右两边。
翻译成点阵的语言,满足最大值原理的点阵:
1两条斜列基一定是菱形等长
2两个基一定是opposed的(实值部分,一正一负,相乘小于0)
3(其实还有第三条,但是作为介绍文,不做计算,我在这里省略了)
从条件1,我们能发现最大值原理允许的点阵的z值一定是在van Iterson diagram上的(其上的每一点,都给出了一个菱形点阵)。这个分岔图给出了随着节间距离y值的变化,允许的发散角x的取值。然后首先考虑节间距离很大,只有最近的一个原基对新生原基有影响的情况,此时新生原基无疑会出现在离最近原基180度的地方,也就是x=1/2处。这对应van Iterson diagram中的垂直线L(见图10)。随着节间距离y的缩小。存在某个y值使得第二近的原基P2开始对新生原基产生影响。这产生了一个分岔点。在这个分岔点A*上,两个原基与一个原基对新生原基的影响应正好效果相同。于是p0和p1的距离,应该和p0p2距离完全相等,见图11,由横向距离为1/2可以求得节间距离, $A^{\star}=(1/2,\sqrt{3}/6) $ 之后允许的点阵z值在 $\sigma_{12},\sigma_{21}$ 上。
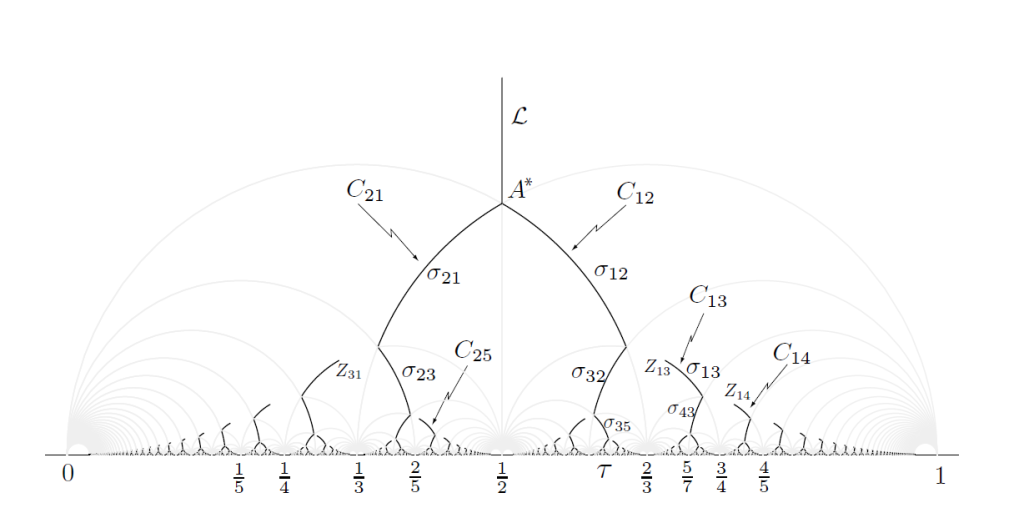
图10
到这里我们还没用上最大值原理的条件2,因为$\sigma_{12},\sigma_{21}$实际上都满足该条件(regular的)。通过计算可以证明,如果一个Q_mn是regular的,其上AB段的弧(双曲几何中的直线)上的每一点z都对应到一组m,n-opposed基。 而如果Q_mn是irregular的,首先B_mn点是不满足opposed基的条件的,而A_mn点始终满足。于是在对于irregularQ_mn,其中从B_mn为起点的某一段弧线必须被排除在外。我们知道$A_{mn}=B_{m+n,n}=B_{m,m+n}$,同时有Q_mn下方的两个双曲四边形必然是一个regular一个irregular,于是在A*之外的每个分岔点上,都会有一条分岔路上的一段被去掉。形成的图形即为图10。每个不连续的独立分支我们有最开始的mn表示为C_mn。从图10我们能看到,所有分支中最大的一个是$C_12,C_21$,观察其上每一段mn字。这正是Fibonacci数列中的元素。随着节间距离的减少,mn值也越来越大,最后趋近的正是黄金率。图10中还有其他更小的分支。每一个分支是一条Fibonacci-like序列,最后收敛于一个无理数,称之为Noble Number。,可以验证的是C13分支在植物中是确实存在的,但已算少见了。至于更小的分支不太清楚。回到为什么Fibonacci系列最多的问题。我想一个额外的原因在于植物在生长过程节间距在不同的时期是不相同的,但是这个变化可能是能够看成连续发生的。包含跨度尽可能大的节间距的C12,C21显然是概率最大分布最广泛的情形。并且C12和L相连,这包括了最初没有原基到有两个原基的过程。多数植物可能都会经历一个这样的阶段,与之连续的C12,C21过程也理应是最容易过度到的状态。PS:发散角为1/2的轮生植物,本身也是相当多的。从现实中能观察到的植物发育和出现的Fibonacci数,似乎y值都较大的。我知道的最大的Fibonacci数都出现在花果中,或许是因为这些部位的原基的生发周期较短。
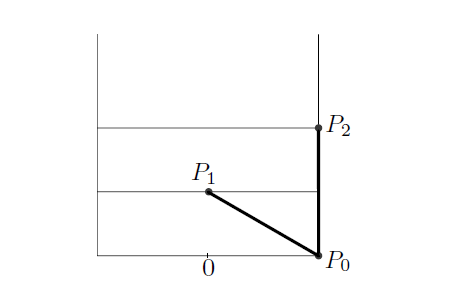
图11
参考文献
[1]Klar A J S. Plant mathematics: Fibonacci’s flowers[J]. Nature, 2002, 417(6889): 595-595.
[2]Douady S, Couder Y. Phyllotaxis as a physical self-organized growth process[J]. Physical review letters, 1992, 68(13): 2098.
[3]Atela, Golé, Hotton. A dynamical system for plant pattern formation: a rigorous analysis[J]. Journal of Nonlinear Science, 2003, 12: 641-676.
[4]Okabe T. Biophysical optimality of the golden angle in phyllotaxis[J]. Scientific reports, 2015, 5(1): 15358.