从Hilda小行星群到模式锁定
Hilda asteroid是一类由5000多颗小行星组成,位于小行星带(asteroid belt)到木星轨道之间的小行星群。他们全体形成的图像看起来像是边略带弧线的三角形(图1),并且三角形的三个顶点刚好处于木星轨道的的三个Lagrange点上,L3,L4,L5。显得十分奇异有趣。(从图1中还能发现两个始终处于L4,L5附近的小行星群,称为特洛伊群(Jupiter trojan))。
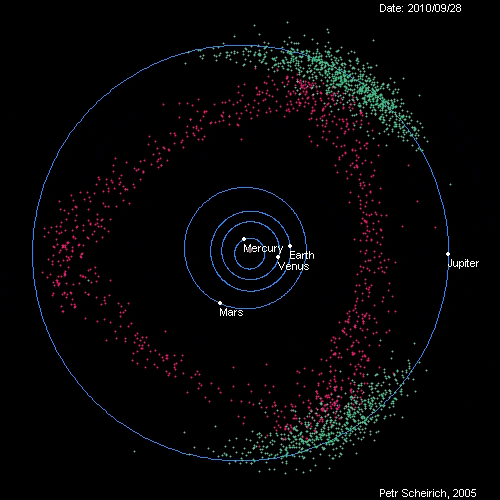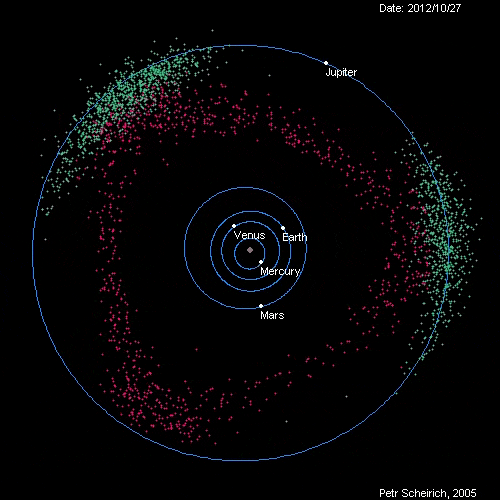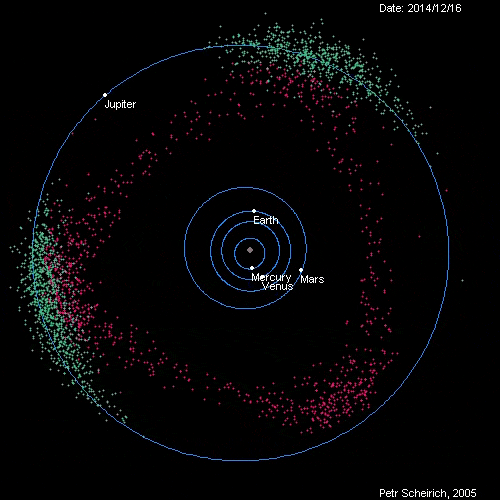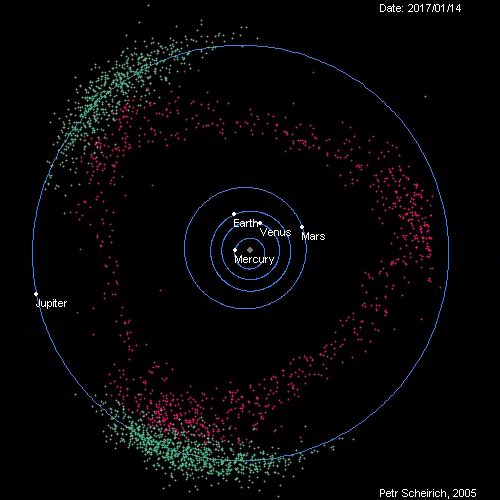
图1 红色为Hilda asteroid 青色为Jupiter trojan
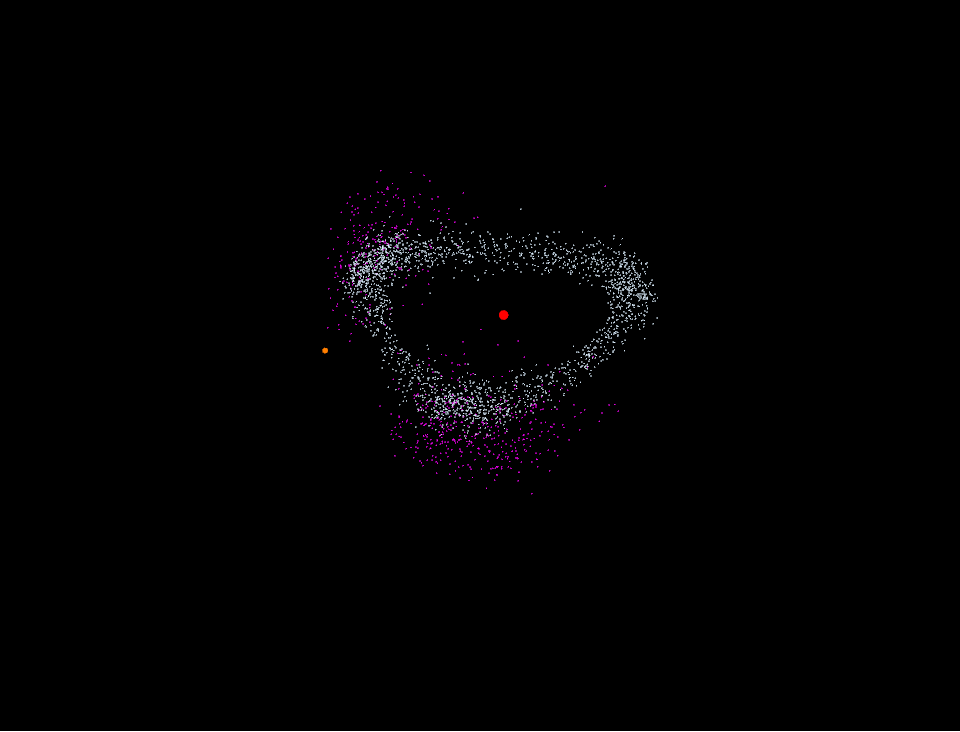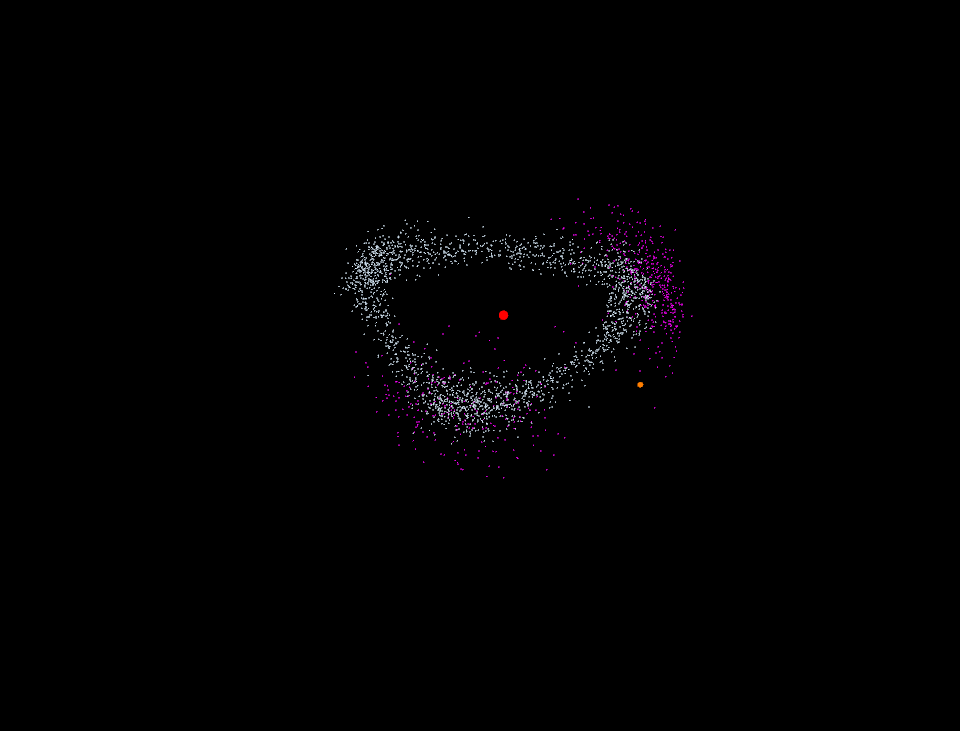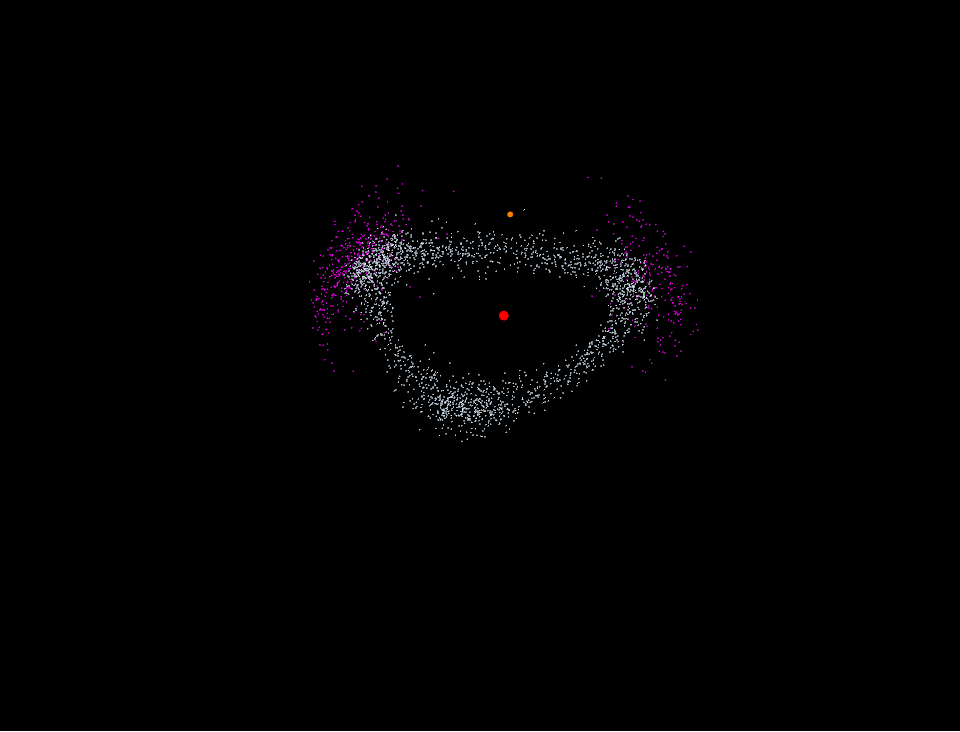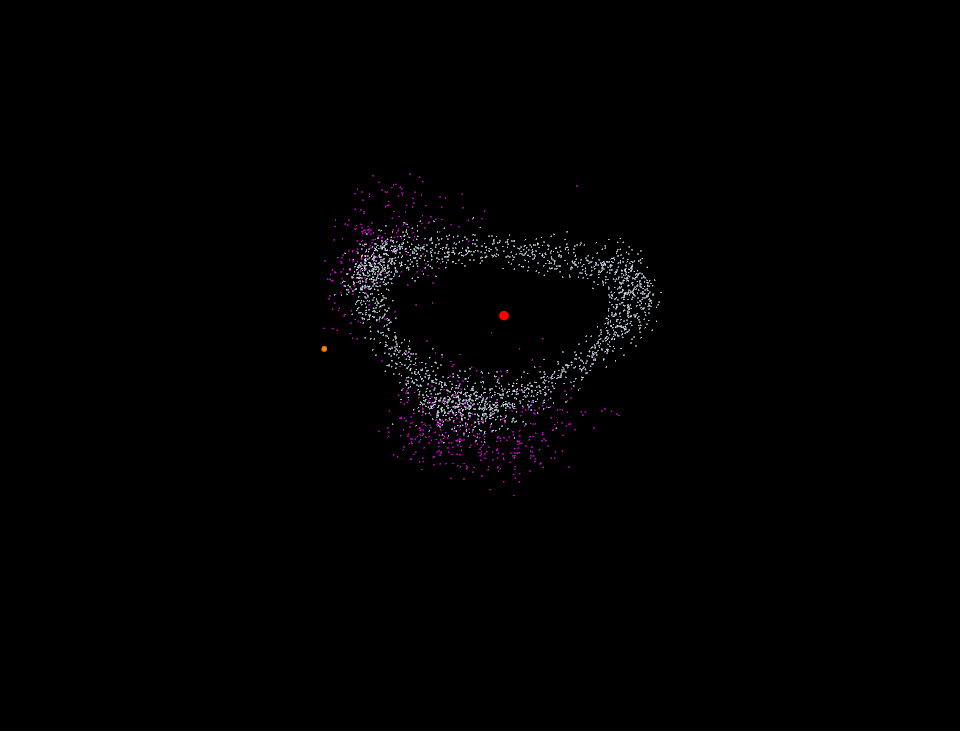
自己用MMA画的Hilda asteroid和Jupiter trojan
但实际上观察单独的某一颗小行星,它的轨迹依旧是椭圆,见图2。小行星与木星的周期比为2:3。并且其轨道的远日点正好在木星的一个Lagrange点附近。木星的L3,L4,L5之间的夹角正好是120度。每当小行星转过一圈回到远地点,木星在相同时间内转过了240度,此时小行星与木星的相对位置虽发生改变,但远日点依旧处于一个Lagrange点附近。
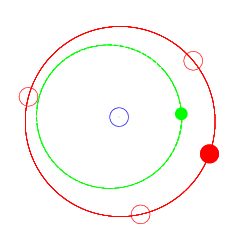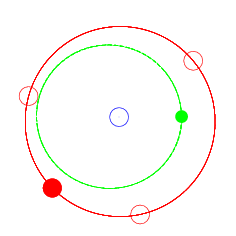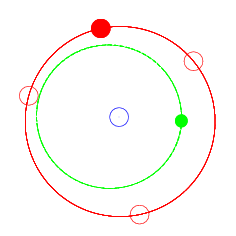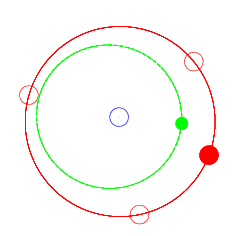
图2 153 Hilda(绿)运动轨迹示意图
像Hilda asteroid与木星这样的整数比轨道(3:2)在天体中很常见,称之为轨道共振,锁频(orbital resonance)。比如,冥王星-海王星的2:3,土星卫星Dione–Enceladus的1:2,同样是土星卫星Hyperion–Titan的3:4,木星卫星Ganymede–Europa–Io的1:2:4。轨道共振除了使得一些特定天体运动变得稳定之外,还可能使某些特定轨道变得不稳定。在这样轨道上的天体很快就会被“抛离”,使得轨道变得空旷。例如土星光环上的间隙,以及木火间小行星带中著名的Kirkwood gaps(图3)
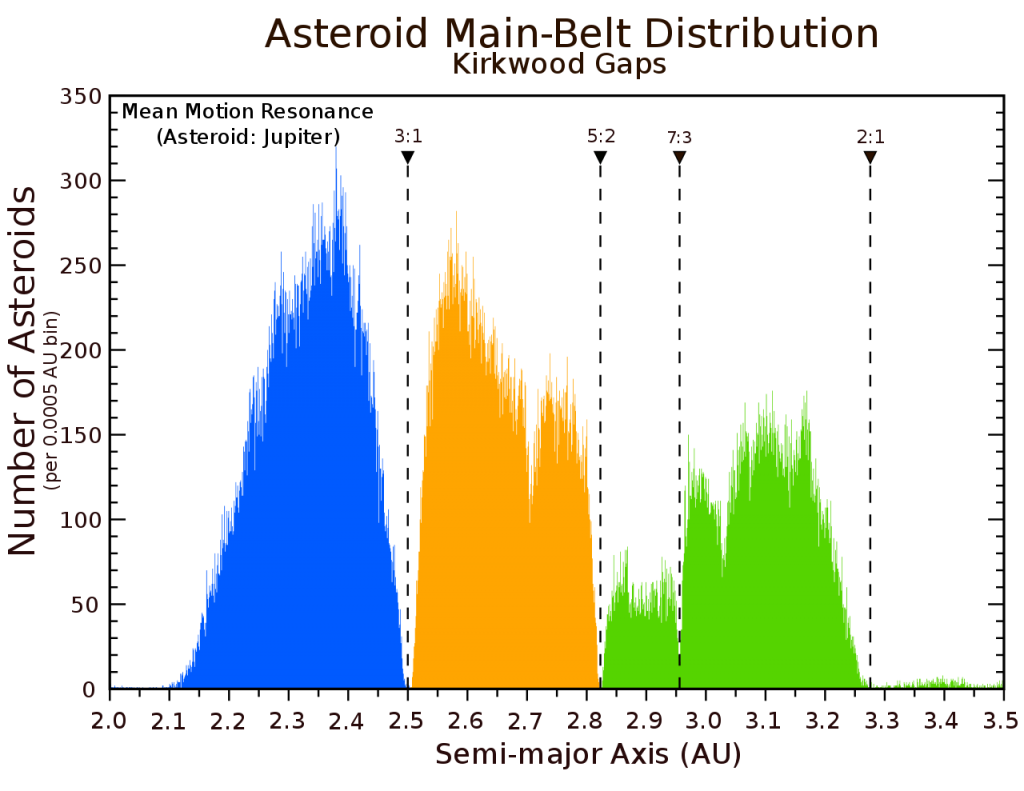
图3 Kirkwood gaps
从这些不算多的数据中我们可以隐隐看出,1:2,1:3,2:3这样的比例出现频率明显较高,而诸如1:8,7:17这样的比例则很少出现,这又是为什么呢?
天体的相互作用还是有点复杂,我们来考虑一个简单些的数学模型。一个circle map $f:S^1\rightarrow S^1$定义为
$$x_{n+1}=f(x_n)=x_n+A+\frac{K}{2\pi}sin(2\pi x_n) \quad mod(1)$$
同时令$F:\mathbb{R}\rightarrow \mathbb{R}$为f的lift ,$x_{n+1}=F(x_n)=x_n+A+\frac{K}{2\pi} sin(2\pi x_n)$
在天体相互作用中,我们可以选取两个天体质量相差巨大的情形,即大天体几乎不受小天体的影响,小天体则受到大天体周期性地影响。取大天体为静止参考系,把大天体对小天体发生一次作用看做f,${x_n}$序列则为小天体的相位,A可看做在一次作用下,大天体使小天体发生的相位变化,为固定值,取值范围为$0\leq A \leq 1 $,$\frac{K}{2\pi} sin(2\pi x_n) $可看做是耦合项或微扰项,其中K的取值范围暂定为$0\leq K \leq 1 $,K完全可以取更大的值,但现象会因此变得更为复杂,故本文中暂且不做讨论。
$f^{(2)}(x)=f(f(x))$表示f的两次迭代,n次迭代同理 。由此我们有
$$f^{(n)}(x_0)=x_0+nA+\sum\limits^{n-1}\limits_{i=0}\frac{K}{2\pi}sin(2\pi x_i) \quad mod(1)$$
为叙述方便,我们令$t^{(n)}=nA+\sum\limits^{n-1}\limits_{i=0}\frac{K}{2\pi}sin(2\pi x_i)$
(1)当K=0:
f简化为$x_{n+1}=f(x_n)=x_n+A$,当A=无理数,${x_n}$是一个伪周期序列。当A=有理数,令$A=p/q$,当n=q,$f^{(n)}(x_0)=x_0+nA \quad mod(1)$,nA=p,是一个整数,所以$f^{(q)}(x_0)=x_0$是一个q周期解。
(2)当$0<K \leq 1 $:
我们定义rotation number u ,$u(f)=\lim\limits_{x \to\infty} \frac{F^{(n)}(x)-x}{n}$。Henri Poincaré首先证明了该极限总是存在且与x的取值无关(没找到那篇1885的文,年代实在久远并且可能是用法文写的,好在证明并不太难)。
——————————–证明的分割线,可跳过——————————–
1)假设极限存在,极限与x取值无关:
由F性质有$F(x+1)=F(x)+1$。设$x<y<x+1<y+1$,由此可得$\frac{F^{(n)}(x)}{n}<\frac{F^{(n)}(y)}{n}<\frac{F^{(n)}(x+1)}{n}<\frac{F^{(n)}(y+1)}{n}$。对上式子各项取极限有$ \lim\limits_{n \to\infty} \frac{F^{(n)}(x)}{n}=\lim\limits_{n \to\infty} \frac{F^{(n)}(y)}{n}$
2)如果f有一个周期点,则极限存在:
假设x是f的一个m周期点。则存在一个整数p,使得$F^{(m)}(x)=x+p$。$F^{(nm)}(x)=x+np$,于是
$$\lim\limits_{n \to\infty} \frac{F^{(nm)}(x)}{nm}=\lim\limits_{n \to\infty} \frac{y+np}{nm}=\frac{p}{m}$$
对任意的整数k,k=rm+q
$$\frac{F^{(k)}(x)}{k}=\frac{F^{(k)}(x)-F^{(rm)}(x)+F^{(rm)}(x)}{k}$$
令$M=max_{0\leq q<m}|F^{(q)}(x)-x|$,有
$$|\frac{F^{(k)}(x)-F^{(rm)}(x)}{k}|\leq \frac{M}{k}$$
于是有
$$\lim\limits_{k \to\infty} \frac{F^{(k)}(x)}{k}=\lim\limits_{n \to\infty} \frac{F^{(rm)}(x)}{rm}=\frac{p}{m}$$
3)如果f没有周期点,极限存在
由假设可知,对任意整数m,$t^{(m)}(x)$不等于整数。令$p_m$为一个整数,满足
$$p_m<F^{(m)}(0)<p_m+1$$
由此可得 $p_m<t^{(m)}(x)<p_m+1$,即 $p_m<F^{(m)}(x)-x<p_m+1$。对$1\leq i\leq n$,有$p_m<F^{(im)}(0)-F^{((i-1)m)}(0)<p_m+1$.将前式i从1取到n相加,可得
$$np_m<F^{(nm)}(0)<n(p_m+1)$$
于是我们知道$\frac{F^{(mn)}(0)}{mn}$和$\frac{F^{(m)}(0)}{m}$都落在相同区间 $(\frac{p_m}{m},\frac{p_m+1}{m})$里。
所以
$$|\frac{F^{(mn)}(0)}{mn}-\frac{F^{(m)}(0)}{m}|\leq 1/m$$
互换m和n,我们有
$$|\frac{F^{(mn)}(0)}{mn}-\frac{F^{(n)}(0)}{n}|\leq 1/n$$ 两式相加 $$|\frac{F^{(m)}(0)}{m}-\frac{F^{(n)}(0)}{n}|\leq 1/m+1/n$$ 所以 $\frac{F^{(n)}(0)}{n}$是一个Cauchy序列,极限存在。
———————————–证明结束———————————
由此我们知道,u(f)是f的某种不变量。 $$
假设u(f)=有理数m/n:
我们把u(f)=m/n的level set记作$M_{m/n}$。
如果$u(f)=m/n$,总存在x使得$F^{(n)}(x)-x=m$,这样的x满足$f^{(n)}(x)=x$,是$f^{(n)}$中的不动点。作为例子,图4,5为$f,f^{(2)}$图像。图中绿色曲线与对角线的交点即为$f^{(n)}(x)=x$。$f^{(n)}$中的不动点,即为f中的n周期点中的一点。图6为某个$t^{(2)}$的图像。容易知道$t^{(n)}(x)-m=0$的根即为对应 $F^{(n)}(x)-x=m$的解。设y为这样的一个根,若$\frac{\partial t^{(n)}(y)}{\partial x}<0$,在后续迭代中,y附近的点将会向y靠近,所以这样的y称为一个稳定点;若$\frac{\partial t^{(n)}(y)}{\partial x}>0$,y附近的点将远离y,这样的点称为不稳定点。同时因为$t^{(n)}(x)$是连续函数,稳定点和不稳定点总是交替出现的(不考虑$\frac{\partial t^{(n)}(y)}{\partial x}=0$)。由此我们可以知道对任意的初值x,如果$u(f)=m/n$,x在经过i*n次f迭代之后,最终会到达某一个稳定点(如果初始就在不稳定点上,则不会改变)。而后进行n周期运动。这也是模型锁定之所以会发生的原因所在,只要处于某一个$u(f)=m/n$的函数下,不论初值为何,最终都将演化为n周期运动。
然后我们在来了解下$M_{m/n}$在参数空间(A,K)的分布情况。如果$M_{m/n}$只是一个或几个孤立的点,那模式锁定无疑也不是容易发生的事情。从现实中的情况来说,我们也已经能猜到情况并非如此。我们已经知道$t^{(n)}(x)-m=0$的根以及$\frac{\partial t^{(n)}(y)}{\partial x}$决定了迭代的性质,这种性质是拓扑的,这些根之间的位置与距离都没有关系。如果我们轻微地改变A,K,根的位置会发生变化,但只要根的数量以及对应的$\frac{\partial t^{(n)}(y)}{\partial x}$符号不发生改变,那么变化后的函数g依旧和变化前的函数f有相同的u,即u(f)=u(g)=m/n。于是这样一簇有相同性质曲线可以用m,n,k刻画,称为$M_{m/n}^{k}$,其中k为稳定点的个数。这样的一个$M_{m/n}^{k}$是参数空间中的连通开集。同时我们立刻可以知道$M_{m/n}$应该包含$\cup^{\infty}{k=1}M{m/n}^{k}$。K=0的f称为$F_0$,为一个点也就是(1)中平凡的情况。可以证明每一个分支$M_{m/n}^{k}$都是与$F_0$连通的。所以$M_{m/n}$是一个连通集。此外在A,K变化至$t^{(n)}(x)-m=0$曲线与x轴相切时,为$M_{m/n}$的边界点。例如u=0,有$A+\frac{K}{2\pi}sin(2\pi x)=0$, 可解得$A=\pm \frac{K}{2\pi}$。即u=0的边界是两条直线。当u为其他分数时,边界就不在是直线了。由于是超越方程无法精确求解。u=1/2的情形,边界可以用$A= \frac{1}{2} \pm \frac{1}{4}(\frac{K}{2\pi})^2$近似。当然实际更简单有效的方法是用计算机算。

图7 图片来源于wiki
其中黄色部分即为$M_{m/n}$,这些结构也被称之为Arnold tongue。从图中我们可以看到0,1,1/2的面积较大,1/4,1/5……随着数字的增大,面积越来越小。这也是模式锁定更容易出现1/2,1/3,2/3,这类小数字比例的原因所在。
然后当$K>1$,从图中也可以猜测出,分属于不同$M_{m/n}$的区块,有可能重叠在一起。于是倍分叉与混沌也将接踵而至,这就是另一个故事了。
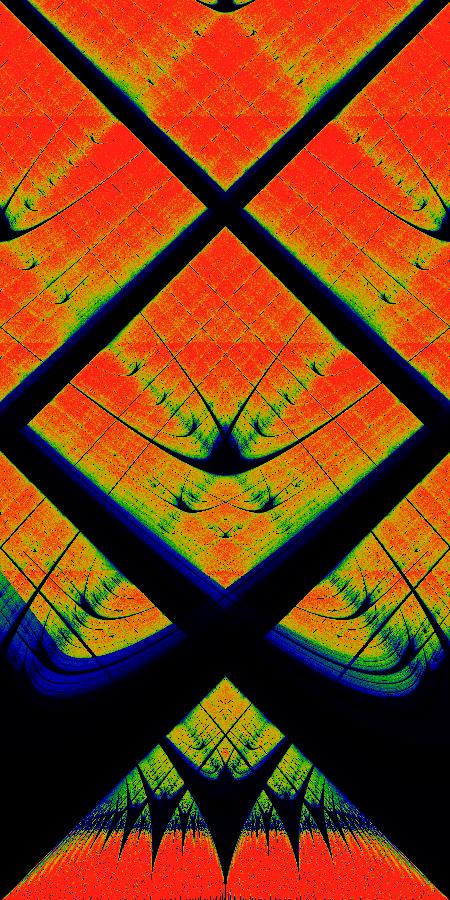
包含k>1的情况 图片同样来源于wiki 有点像eva中出现的画面呢(误)

自己用MMA画的
可参考的文献:
Arnold V I. Small denominators. I. Mapping of the circumference onto itself[J]. Collected Works: Representations of Functions, Celestial Mechanics and KAM Theory, 1957–1965, 2009: 152-223.
开山论文,本文所使用的circle map只是经典且普遍的一个特例。Arnold在论文中的讨论更加普适。原文是俄文转英
Glass L, Perez R. Fine structure of phase locking[J]. Physical Review Letters, 1982, 48(26): 1772.
PRL上的短文,介绍了K>1的情况。